Messgrößen für Prognosen

Allgemein

Die Genauigkeit von Prognosen ist ein Kriterium zur Bewertung der Eignung eines bestimmten Prognoseverfahrens für eine bestimmte Datengruppe. Die Prognosegenauigkeit ist der Hauptgrund, um ein Prognoseverfahren einem anderen vorzuziehen. Auch die Einstellung der Parameter für ein bestimmtes Verfahren dient der Prognosegenauigkeit. Die Prognosegenauigkeit gibt an, wie zuverlässig ein aktuelles Prognoseverfahren in der Lage ist, bekannte Daten zu reproduzieren.

Sechs Messgrößen zur Messung der Prognosegenauigkeit sind definiert und quantifiziert: MAE, ME, MAPE, PVE, Verfolgungssignal und Theils U-Statistik. Der Determinationskoeffizient ist verfügbar, wenn eines der Regressionsmodelle ausgeführt wird. Die Prognosemodelle können basierend auf dem Wert einer oder mehrerer dieser Messungen beurteilt werden.

Notation

n	Anzahl der Beobachtungen.
Dt	In Periode t beobachteter Bedarf.
FT	Prognose in Periode t.
D	Delta (Glättungsparameter des Verfolgungssignals).
et	= Dt - Ft

Die verfügbaren Messgrößen sind:

1. MAE
2. Wert/MAE
3. ME
4. RME
5. MAPE
6. WMAPE
7. MSE
8. Varianzbedarf
9. PVE
10. Verfolgungssignal
11. Anpassungsfaktor
12. Leistungsfaktor
13. R Quadrat
14. Quadrat des Mittelwerts von R
15. Service-Ebene
16. Füllquote Service
    

MAE

MAE ist der mittlere absolute Fehler (mean absolute error). Dabei gilt folgende Umrechnungsformel:

Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

Wert/MAE

Der MAE-Wert entspricht dem Produkt von MAE und Bestandswert für den Artikel. Für prognostizierte Artikel mit einem hohen MAE-Wert ist eine höhere Genauigkeit besonders profitabel.

ME

ME ist der mittlere Fehler (mean error). Dabei gilt folgende Umrechnungsformel:

Die Aussagekraft des ME-Kriteriums ist relativ begrenzt, da positive und negative Fehler sich gegenseitig aufheben. Mit ME lässt sich nur feststellen, ob eine systematische Über- oder Unterprognostizierung vorliegt, die auch systematischer Prognosefehler genannt wird. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

RME

RME ist die Abkürzung für relativer mittlerer Fehler (relative mean error). Dabei gilt folgende Umrechnungsformel:

<![if!msEquation]> <![if!vml]>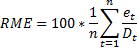<![endif]><![endif]>

Die Aussagekraft des RME-Kriteriums ist begrenzt, da positive und negative Fehler sich gegenseitig aufheben. Mit RME lässt sich nur feststellen, ob eine systematische Über- oder Unterprognostizierung vorliegt, die auch systematischer Prognosefehler genannt wird. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben) Der Artikel mit dem höchsten RME ist der Artikel, der die höchste Varianzprognose hat.

Abweichungen in der Prognose weisen darauf hin, dass Sie konstant bis optimistisch (Überprognostizierung negativer RME) oder pessimistisch (Unterprognostizierung positiver RME) sind.

MAPE

MAPE ist die Abkürzung für den mittleren absoluten prozentualen Fehler, die Formel lautet wie folgt:

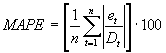
MAPE drückt für jeden Artikel die relative Ungenauigkeit in einer Prognose aus. Elemente mit dem höchsten MAPE sollten von höherer Prognosegenauigkeit profitieren. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

WMAPE

WMAPE ist die Abkürzung für den gewichteten mittleren absoluten prozentualen Fehler, die Formel lautet wie folgt:

WMAPE drückt für jeden Artikel die relative Ungenauigkeit für jede Position in einer Prognose aus. Perioden mit großen absoluten Fehlern erhalten mehr Gewicht als Perioden mit kleinen absoluten Fehlern. Dadurch ist es nicht möglich, dass Perioden mit kleinen absoluten Fehlern aber hohen Prozentsatzfehlern die Messung dominieren. Elemente mit dem höchsten WMAPE sollten von höherer Prognosegenauigkeit profitieren. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

MSE

MSE ist die Abkürzung für den mittleren quadrierten Fehler, die Formel lautet wie folgt:

<![if!msEquation]> <![if!vml]>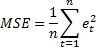<![endif]><![endif]>

MSE drückt für jeden Artikel die quadrierte Ungenauigkeit in einer Prognose aus. Elemente mit dem höchsten MSE sollten von höherer Prognosegenauigkeit profitieren. Artikel mit einzelnen großen Prognosefehlern haben einen höheren MSE-Wert als ein Artikel, der den gleichen Prognosefehler aufweist, der aber gleichmäßiger über die Berechnungsperiode hinweg verteilt ist. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

Bedarfsvarianz

Dies ist die Abweichung vom Durchschnitt im Bedarfsvektor, die Formel lautet wie folgt:

<![if!msEquation]><![if!vml]><![endif]><![endif]>

Die Abweichung gibt die Variation im Bedarfsmuster des Artikels an. Artikel mit hoher Bedarfsvarianz sind in der Regel nur schwer zu prognostizieren und erfordern ggf. zusätzliche Aufmerksamkeit. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

PVE

PVE ist der prozentuale Anteil der erklärten Abweichung (percentage variation explained). Die Formeln lauten wie folgt:

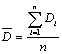
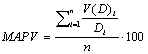
PVE gibt an, welcher Anteil der inhärenten Abweichung des Bedarfs durch das Prognoseverfahren erklärt wird. PVE zeigt an, ob die Prognose im Lauf der Zeit besser oder schlechter wird, da Änderungen in Bedarfsschwankungen korrigiert werden. Außerdem ist der Wert eine gute Vergleichsmessgröße. Falls PVE kleiner als 0 ist, erhöht die Prognose die Bedarfsabweichung. In diesem Fall empfiehlt es sich, das Prognoseverfahren zu ändern oder die Parameter anders einzustellen (Alpha oder die Anzahl der Perioden für den gleitenden Durchschnitt erhöhen).

Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

Verfolgungssignal

Das Verfolgungssignal ist eine Methode, um systematische Fehler festzustellen und auf Änderungen im Bedarfsmuster zu reagieren. Ein hohes Verfolgungssignal (d.h, > 0,6) lässt vermuten, dass die Prognose einen systematischen Fehler aufweist. Je niedriger der Delta-Wert, desto geringer das Risiko eines falschen Alarms (Warnmeldungen werden später ausgegeben als bei einem hohen Delta-Wert). Es wird ein Delta-Wert zwischen 0,1 und 0,3 empfohlen. Die Formeln lauten wie folgt:

Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

Anpassungsfaktor

Anpassungsfaktor, die Formel lautet wie folgt:

<![if!msEquation]> <![endif]>

Der Anpassungsfaktor drückt Differenz zwischen der vom Anwender angepassten Prognose (historische Prognose) und einer rein mathematischen Prognose (Erklärungsprognose) aus. Ein Anpassungsfaktor 10 bedeutet, dass der Anwender die Prognose i 10 % genauer angepasst hat als die rein mathematische Prognose; -10 bedeutet, dass die rein mathematische Prognose besser ist. Elemente mit hohem negative Änderungsfaktor sollten eine reine mathematischen Prognose (automatische) nutzen. Diese Formel wird für die letzte historische Periode und die Anzahl der angegeben Prognosefehlerperioden in der Vergangenheit ausgeführt (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

Leistungsfaktor

Leistungsfaktor, die Formel lautet wie folgt:

<![if !vml]>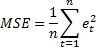<![endif]>

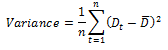
Varianz ist die Variation des Bedarfsmusters des Artikels. Positionen mit hoher Bedarfsvarianz erfordern besondere Aufmerksamkeit, da sie schwer prognostizierbar sind.

MSE ist eine Abkürzung für Mean Squared Error (mittlerer quadratischer Fehler) und drückt das Quadrat der Ungenauigkeit in der Prognose für jedes Objekt aus. Objekte mit dem höchsten MSE sollten von höherer Prognosegenauigkeit profitieren.

Objekte mit einem hohen Leistungsfaktor müssen aufmerksam behandelt werden. Im Vergleich zur Bedarfsabweichung ist die prognostizierte Genauigkeit für solche Objekte gering. Ein Leistungsfaktor über 1 bedeutet, dass die Abweichung des tatsächlichen Bedarfs von der Prognose höher ist als die Schwankungen des Bedarfs aus dem Durchschnitt. Diese Formel wird für die letzte historische Periode ausgeführt, und n ist die Anzahl der Perioden, die in den Prognosefehlerperioden vorher angegeben wurde (n = Prognosefehlerperioden). (Siehe Allgemeine Server-Daten eingeben)

R Quadrat

Auch als R2 bezeichnet. Diese Messgröße wird nur dann herangezogen, wenn als Prognosemodell eine Regression (Methode der kleinsten Quadrate) oder eine Mehrfachregression verwendet wird. R-Quadrat lässt sich als die Proportion der Varianz im historischen Bedarf interpretieren, der durch die Regression (mit der Methode der kleinsten Quadrate) oder die ausgewählten Erklärungsvariablen (bei mehrfacher Regression) erklärbar ist.

Notation:

Yi	Regressionsschätzung der Bedarfsvariablen.
Di	Die Bedarfsvariable.

<![if !vml]><![endif]>

<![if!msEquation]> <![if !vml]><![endif]>

Service-Ebene

Die Service-Ebene zeigt den Prozentsatz der Tage, an denen das Produkt innerhalb von Prognosefehlerperioden für den Kunden verfügbar war. Ein Tag wird als „ausverkauft“ betrachtet, wenn an diesem Tag keine Verkäufe gemeldet wurden und die Lagermenge am Ende des Tages 0 (null) beträgt. Das Maß des Service Levels wird wie folgt berechnet:

<![if!msEquation]> <![if!vml]><![endif]><![endif]>

Füllquote Service

Die Füllquote Service ist der Prozentsatz der durch den Kunden angeforderten Menge, der durch die Einheit innerhalb der Prognosefehlerperioden abgedeckt ist. Dies ist das Verhältnis zwischen der gelieferten Menge und der von Kunden angeforderten Gesamtmenge. Hierdurch erhält der Anwender eine Vorstellung vom Prozentsatz der angenommenen Verkäufe aufgrund der Produktverfügbarkeit für den Kunden. Das Maß der Füllquote Service wird wie folgt berechnet.

<![if !vml]><![endif]>

<![if !msEquation]> <![if !vml]><![endif]><![endif]>

Die verlorene Menge ist der in Ausverkauf-Tage erwartete Bedarf. Ein Tag wird als „Ausverkauft“ betrachtet, wenn an diesem Tag keine Verkäufe erfasst wurden und die Lager-/Bestandsmenge am Ende des Tages 0 (Null) beträgt. Der Betrag der verlorenen Menge der Ausverkauf-Tage kann mithilfe der Systemprognose oder der angepassten Prognose berechnet werden. Es gibt eine erweiterte Servereinstellung, bei der der Anwender die Möglichkeit hat, aus den beiden oben genannten Optionen die bevorzugte Option für die Berechnung der Kompensation für Ausverkauf-Tage (verlorene Menge) auszuwählen. Die Systemprognose ist die Standardmethode für die Berechnung der Kompensation für Ausverkauf-Tage.

<![if!msEquation]> <![endif]>